¿Tienes problemas con los circuitos digitales? ¡Este artículo sobre Karnaugh Maps lo ayudará a simplificar funciones lógicas complejas!

En este artículo, analizaré cómo puede usar los mapas de Karnaugh para simplificar funciones lógicas complejas para la implementación en un circuito digital. Tenga en cuenta que esto es solo un resumen del tema y que hay mucho más que cubrir. Sin embargo, debería darle una buena visión general para que pueda comenzar a diseñar circuitos digitales simples de inmediato.

Para mantener este artículo breve, supondré que ya sabe cómo contar en binario y cómo puede convertir números decimales en valores binarios y viceversa. Si necesita un repaso, consulte la numeración decimal versus binaria que cubre más a fondo los temas.

Una visión general de las puertas lógicas

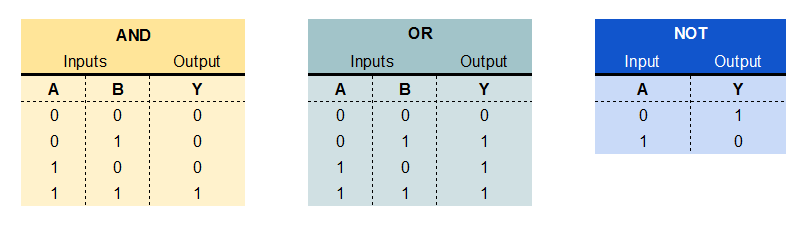
Las funciones lógicas más simples son NOT, AND y OR. Puede derivar cualquier otra función lógica combinando la función NOT con AND u OR.

Una puerta lógica que implementa la función AND emite un estado ALTO si y solo si todas las entradas son ALTAS al mismo tiempo. Una puerta OR emite un 1 binario si al menos una de sus entradas es ALTA. Una puerta NOT genera un 1 binario si la entrada es BAJA y viceversa.

Leer y crear tablas de verdad

En las tablas de verdad anteriores, cada entrada tiene su propia columna y se representa cada combinación posible de valores de entrada. La salida siempre se indica para una combinación de señales de entrada. Para crear una tabla de verdad, comience escribiendo todas las combinaciones de entrada posibles. A continuación, determine cómo desea que se comporten sus resultados para cada patrón.

Ejemplo de tabla de verdad

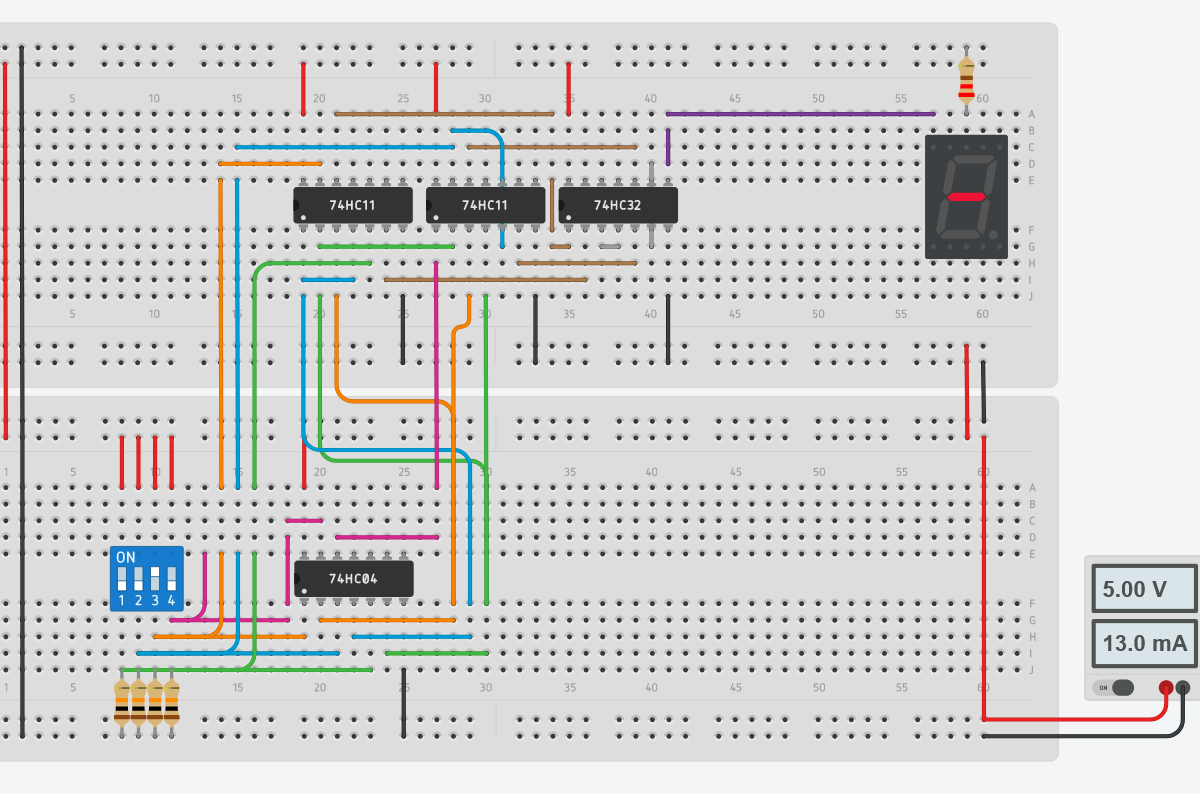
Quiero construir un circuito digital que pueda generar un solo número decimal en una pantalla de siete segmentos. Para lograr esto, primero tenemos que determinar qué segmentos deben activarse para cada número. Sabiendo esto, creé la siguiente tabla de verdad.

Ahora, si inspeccionamos G, podemos ver qué combinaciones de entrada debe haber habilitado la salida (el guión en el centro de la pantalla de siete segmentos).

Una vez que haya creado una tabla de verdad, debe encontrar una fórmula lógica que represente la función de salida. La forma más fácil de hacer esto es completar un mapa de Karnaugh.

Cómo crear mapas de Karnaugh

En un mapa de Karnaugh, cada celda representa una combinación de valores de entrada, mientras que el valor de cada celda representa el estado binario correspondiente de la salida.

En este ejemplo, tenemos cuatro entradas, y el mapa K consta de cuatro filas y cuatro columnas donde las entradas están alineadas, como se ve en la imagen a continuación.

Nota: El mapa de Karnaugh será diferente si cambia la cantidad de entradas.

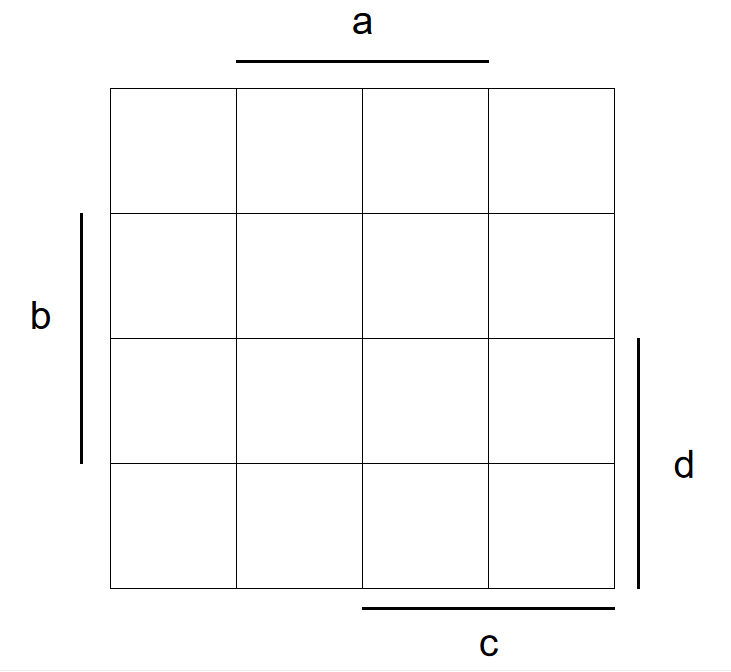
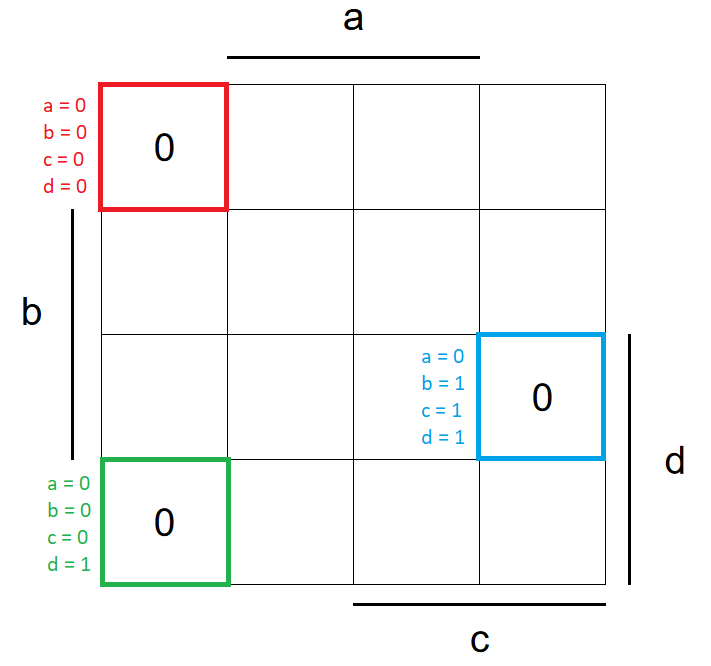
Los 16 campos en el mapa corresponden a las 16 combinaciones diferentes de las cuatro señales de entrada (ad) en la tabla de verdad. Como puede ver, algunas columnas y filas están etiquetadas con letras. En esas filas y columnas, la variable de entrada correspondiente tiene un valor de uno. De lo contrario, esta variable tiene un valor de cero.

Por lo tanto, la entrada 0111 (a = 0, b = 1, c = 1, d = 1) está representada por esta celda en el mapa:

La entrada 0111 (a = 0, b = 1, c = 1, d = 1) está representada por la celda resaltada en el mapa.

Ahora necesitamos completar el valor de la salida para cada combinación de entrada posible.

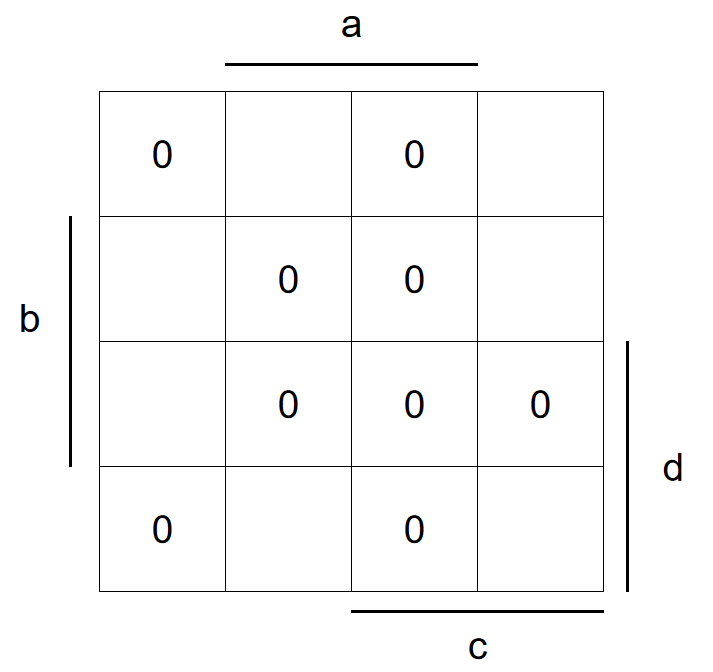
Comencemos con aquellos donde G es cero. Tenga en cuenta que este es el caso cuando todas las entradas son BAJAS en la tabla de verdad anterior. Los otros dos casos válidos donde el resultado es cero, son 0001 y 0111 (que se muestran a continuación).

A continuación, cubriré todos los estados no válidos. Esas son todas las entradas que no representan un número decimal de un solo dígito. Si las entradas representan un estado no válido, cada segmento debe estar apagado.

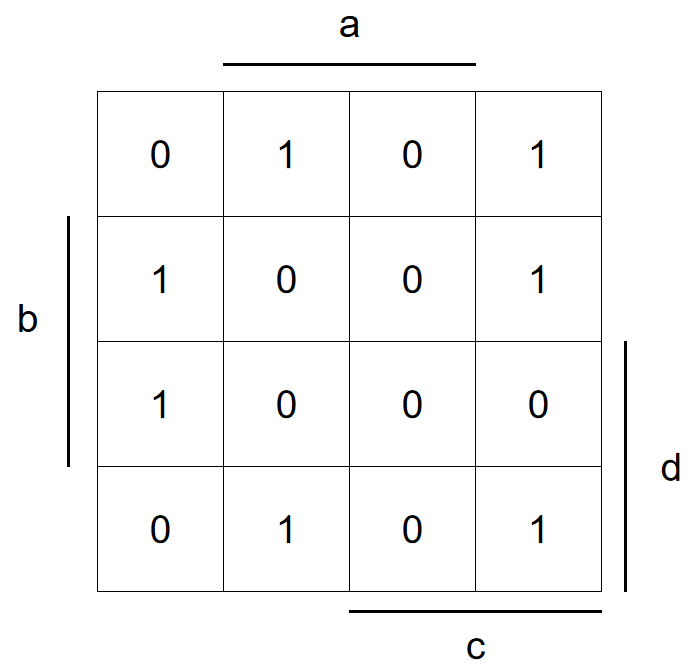
En todos los casos restantes, G tiene un valor de uno, lo que facilita completar la matriz.

Derivar una fórmula de salida

Para determinar una fórmula de salida simplificada, tenemos que encontrar grupos de celdas adyacentes que tengan el mismo valor. Estos grupos deben tener un área que tenga una potencia de dos (uno, dos, cuatro, ocho, etc.), y no tenemos que parar en los bordes de la matriz. 

Entonces, en este mapa, podría encontrar los siguientes grupos en unos (también podríamos agrupar ceros pero no discutiré ese enfoque aquí):

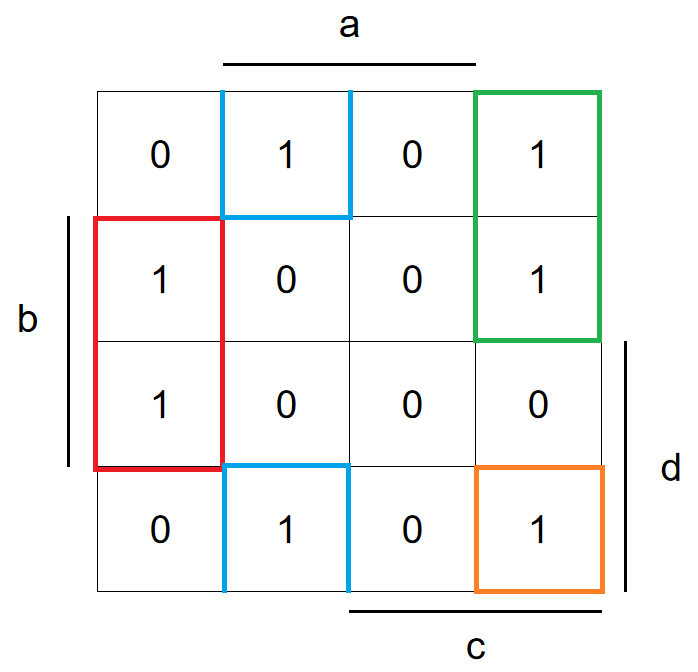
Como puede ver, el grupo azul se envuelve al otro lado de la matriz, para formar un área más grande en lugar de dos más pequeñas. En general, deberíamos intentar formar el grupo más grande posible, lo que resultará en una función más simple al final. Tenga en cuenta que los grupos diagonales no están permitidos.

Para derivar la fórmula, observe la posición de cada grupo en la matriz individualmente. El grupo rojo, por ejemplo, está situado en los campos (NO a) y (b) y (NO d) y (d) y (NO c), que se describe mediante la siguiente fórmula:

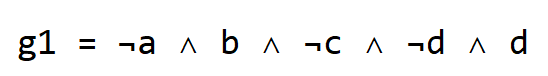
Podemos simplificar esta fórmula eliminando (NO d) y d. Ahora, repita este proceso para todos los otros grupos. Deberíamos terminar con estas cuatro expresiones (ya simplificadas):

Una vez que tengamos esos, solo necesitamos conectarlos con expresiones OR para obtener la fórmula final para la salida G:

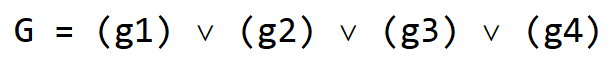
Esta es una fórmula que podemos implementar fácilmente con puertas lógicas para construir un circuito digital: